Inferensi dalam logika order pertama

22.06 |

Definisi Proposisi

Proposisi adalah pernyataan tentang hubungan yang terdapat di antara subjek dan predikat. Dengan kata lain, proposisi adalah pernyataan yang lengkap dalam bentuk subjek-predikat atau term-term yang membentuk kalimat. Kaliimat Tanya,kalimat perintah, kalimat harapan,dan kalimat inversi tidak dapa disebut proposisi. Hanya kalimat berita yang netral yang dapat disebut proposisi. Tetapi kalimat-kalimat itu dapat dijadikan proposisi apabila diubah bentuknya menjadi kalimat berita yang netral.

Jenis-Jenis Proposisi

Proposisi dapat dipandang dari 4 kriteria, yaitu berdasarkan :
• Berdasarkan bentuk
Berdasarkan bentuk dapat dibagi menjadi 2, yaitu :

Tunggal adalah proposisi yang terdiri dari satu subjek dan satu predikat atau hanya mengandung satu pernyataan.
Contoh :
o Semua petani harus bekerja keras.
o Setiap pemuda adalah calon pemimpin

Majemuk atau jamak adalah proposisi yang terdiri dari satu subjek dan lebih dari satu predikat.
contoh :
o Semua petani harus bekerja keras dan hemat.
o Paman bernyanyi dan menari.

Modus Ponen

Modus ponen adalah salah satu cara pengambilan kesimpulan (argumentasi) yang paling sederhana dan dibenarkan secara kaidah logika dan mungkin adalah yang paling sering kita gunakan. Dia bekerja berdasarkan premis kalimat majemuk jika p maka q.
Contoh :
Premis1 : Hewan Mamalia Bernafas dengan paru-paru
Premis2 : Hewan ini adalah hewan mamalia
Kesimpulan : Hewan ini bernafas dengan paru-paru
Modus ponen ini sangat dekat dengan motode deduktif yang akan dibahas nanti. Dalam contoh di atas, karena kita tahu bahwa ikan paus adalah hewan mamalia, maka melalui deduktif kita bisa simpulkan ikan paus juga bernafas dengan paru-paru. Lebih detilnya silakan baca artikel berikut

Unifikasi

Unifikasi adalah usaha untuk mencoba membuat dua ekspresi menjadi identik (mempersatukan keduanya) dengan mencari substitusi-substitusi tertentu untuk mengikuti peubah-peubah dalam ekspresi mereka tersebut. Unifikasi merupakan suatu prosedur sistematik untuk memperoleh peubah-peubah instan dalam wffs. Ketika nilai kebenaran predikat adalah sebuah fungsi dari nilai-nilai yang diasumsikan dengan argumen mereka, keinstanan terkontrol dari nilai-nilai selanjutnya yang menyediakan cara memvalidasi nilai-nilai kebenaran pernyataan yang berisi predikat. Unifikasi merupakan dasar atas kebanyakan strategi inferensi dalam Kecerdasan Buatan. Sedangkan dasar dari unifikasi adalah substitusi.

Suatu substitusi (substitution) adalah suatu himpunan penetapan istilah-istilah kepada peubah, tanpa ada peubah yang ditetapkan lebih dari satu istilah. Sebagai pengetahuan jantung dari eksekusi Prolog, adalah mekanisme unifikasi.

Aturan-aturan unifikasi :

1. Dua atom (konstanta atau peubah) adalah identik.

2. Dua daftar identik, atau ekspresi dikonversi ke dalam satu buah daftar.

3. Sebuah konstanta dan satu peubah terikat dipersatukan, sehingga peubah menjadi terikat kepada konstanta.

4. Sebuah peubah tak terikat diperssatukan dengan sebuah peubah terikat.

5. Sebuah peubah terikat dipersatukan dengan sebuah konstanta jika pengikatan pada peubah terikat dengan konstanta tidak ada konflik.

6. Dua peubah tidak terikat disatukan. Jika peubah yang satu lainnya menjadi terikat dalam upa-urutan langkah unifikasi, yang lainnya juga menjadi terikat ke atom yang sama (peubah atau konstanta).

7. Dua peubah terikat disatukan jika keduanya terikat (mungkin melalui pengikatan tengah) ke atom yang sama (peubah atau konstanta).

· Forward Chaining

Forward chaining merupakan metode inferensi yang melakukan penalaran dari suatu masalah kepada solusinya. Jika klausa premis sesuai dengan situasi (bernilai TRUE), maka proses akan menyatakan konklusi. Forward chaining adalah data-driven karena inferensi dimulai dengan informasi yang tersedia dan baru konklusi diperoleh. Jika suatu aplikasi menghasilkan tree yang lebar dan tidak dalam, maka gunakan forward chaining.

Contoh :

Terdapat 10 aturan yang tersimpan dalam basis pengetahuan yaitu :

R1 : if A and B then C

R2 : if C then D

R3 : if A and E then F

R4 : if A then G

R5 : if F and G then D

R6 : if G and E then H

R7 : if C and H then I

R8 : if I and A then J

R9 : if G then J

R10 : if J then K

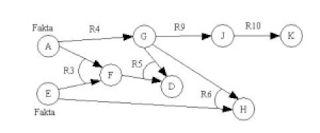
Fakta awal yang diberikan hanya A dan E, ingin membuktikan apakah K bernilai benar. Proses penalaran forward chaining terlihat pada gambar dibawah :

Gambar Forward Chaining

· Backward Chaining

Menggunakan pendekatan goal-driven, dimulai dari harapan apa yang akan terjadi (hipotesis) dan kemudian mencari bukti yang mendukung (atau berlawanan) dengan harapan kita. Sering hal ini memerlukan perumusan dan pengujian hipotesis sementara. Jika suatu aplikasi menghasilkan tree yang sempit dan cukup dalam, maka gunakan backward chaining.

Contoh :

Seperti pada contoh forward chining, terdapat 10 aturan yang sama pada basis pengetahuan dan fakta awal yang diberikan hanya A dan E. ingin membuktikan apakah K bernilai benar. Proses penalaran backward chaining terlihat pada gambar berikut :